Ramanujan and Magic Squares
Srinivasa Ramanujan had a special affinity toward numbers. His taxi-cab number (1729) incident is popular. A Mathematician without parallel, he made extraordinary contributions to mathematical analysis, number theory, infinite series, and continued fractions. His works have been collected and analyzed throughout the world
Incidentally, in the opening page of the first Ramanujan’s notebook, there begins by working out a 3 x 3 Magic Square!
Having worked on a variety of special Magic squares ourselves, we could not think of a greater tribute to Srinivasa Ramanujan than this!
Summary
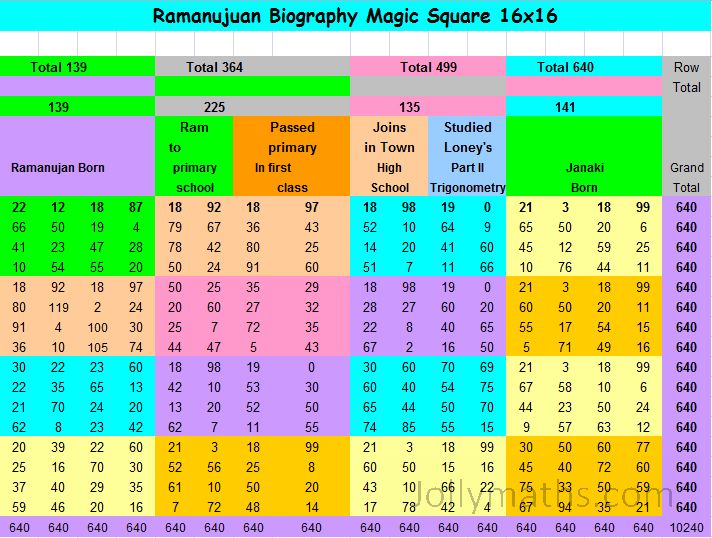
This is one of the biggest number puzzles we have done so far! This Biography Magic Square summarizes the important events that happened in the life of Sri Srinivasa Ramanujan.
The important dates in the life of Srinivasa Ramanujan were compiled from various sources. These dates were taken two digits at a time, representing either the date of the month or the month or the first/second half of the four-digit year. As an example, Ramanujan’s date-of-birth 22-12-1887, is taken as four separate entries as 22 12 18 and 87. In short, Ramanujan’s entire life history is reproduced here, from his birth to till date in Ramanujan-style.

Construction
Important dates from Ramanujan’s life were collected and these were then arranged horizontally in a row, from left to right. This row would form the top row of this biography magic square. The rest of the magic square is constructed after assembling this row.
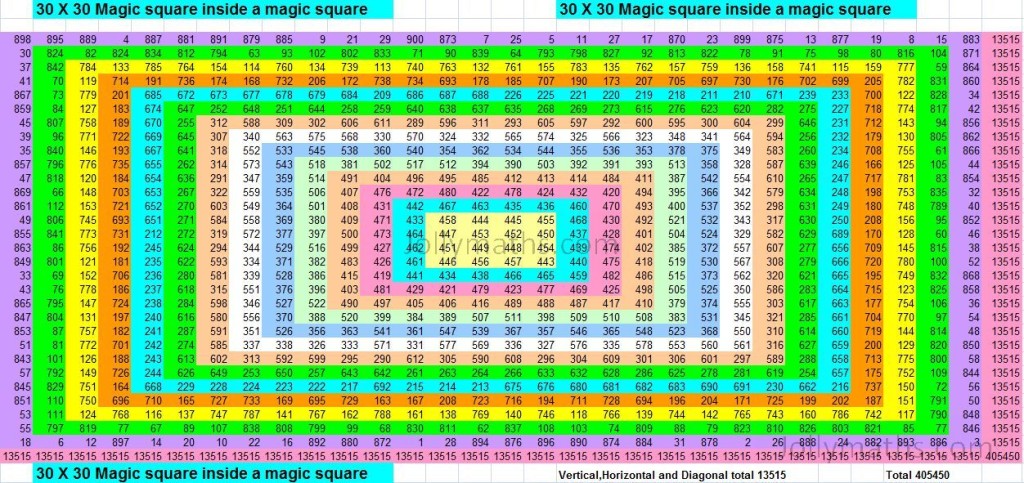
This magic square has the properties of a conventional magic square, namely the sum of the entries along each row/column/diagonal sum up to the same magic-sum 2183.
It has these additional properties:
– starting from left to right, or, from top to bottom, we have embedded magic squares of orders 4 x 4 , 8 x 8, 12 x 12, 16 x 16, 20 x 20, and then in increased orders of 25 x25, 30 x 30, 36 x 36, 42 x 42, 49 x 49, 56 x 56, 64 x 64, 72 x 72, 81 x 81, 90 x 90, and finally 100 x 100. This is thus a cascade of magic-squares-inside-a-magic-sqaure!
Thus the total 100 x 100 Ramanujan Biography Magic square will contain the following 184 smaller magic squares of sizes as listed below:
Size of Magic Square Number of such Magic Squares Total Entries
4 x 4 Magic squares 25 25 ( 4 x 4 ) = 400 squares
5 x 5 Magic squares 20 20 ( 5 x 5 ) = 500 squares
6 x 6 Magic squares 24 24 ( 6 x 6 ) = 864 squares
7 x 7 Magic squares 28 28 ( 7 x 7 ) = 1372 squares
8 x 8 Magic squares 32 32 ( 8 x 8 ) = 2048 squares
9 x 9 Magic squares 36 36 ( 9 x 9 ) = 2916 squares
10 x 10 Magic squares 19 19 (10 x 10 ) = 1900 squares
Total 184 (Different sized squares) 10,000 Squares
Sidenote
We have constructed a smaller 16 x 16 version of this Biography Magic Square with fewer details, which you can find here.
This was earlier published in an article “A Unique Novel Homage to the Great Indian Mathematician” in the March 2013 (Volume 23, Pg 146-147) Mathematics Newsletter published by the Ramanujan Mathematics Society. (download free).