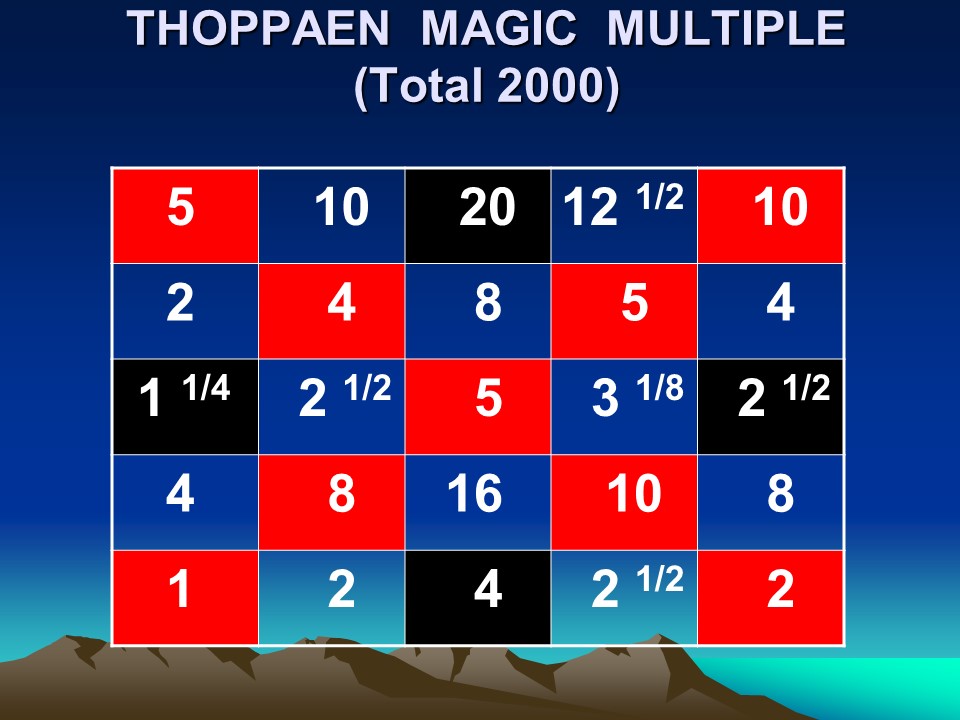
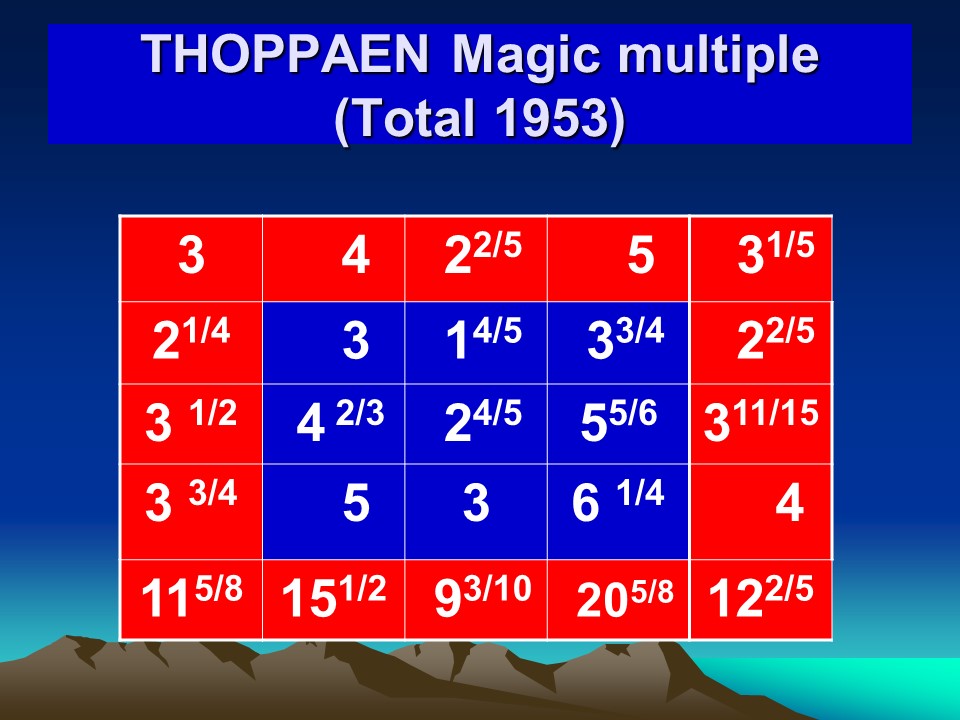
All fractions are fraction only. (Not to the power)
Enjoy the puzzle in more and more methods . Share the joyous occasions with others
Thoppaen Magic Multiple
God’s Magic square
Generally a magic square is a square of any size “n x n ” filled with numbers. And after filling the numbers the Vertical, Horzontal and both diagonal totals must be equal.
In general the row total will be smallest number added with the highest number and divided by two, and then multiplied by the number of rows.
This is the minimum condition for any magic square in general.
In this above single square Magic square,
The vertical total is ONE, the Horizontal total is ONE and both Diagonal totals are also ONE
Finally as per the total formula also, 1 + 1 = 2 / 2 = 1 x 1 = 1.
It is satisfying all the conditions of a magic square.
This is called as God’s Magic Square
Puzzling number Puzzles
There are many different kinds of puzzles for entertainment as well as to improve our knowledge as well.
In the above You have to write all numbers from 1 to 9 in the same arrangement and you can put any mathematical symbol as you know.
The result of the final format must be 100.
Remember. There are 320 different methods available.
Some of the solutions are given here for easy understanding.
Hope you will be finding this puzzle is very challenging and enjoyable.
Reverse Magic Square
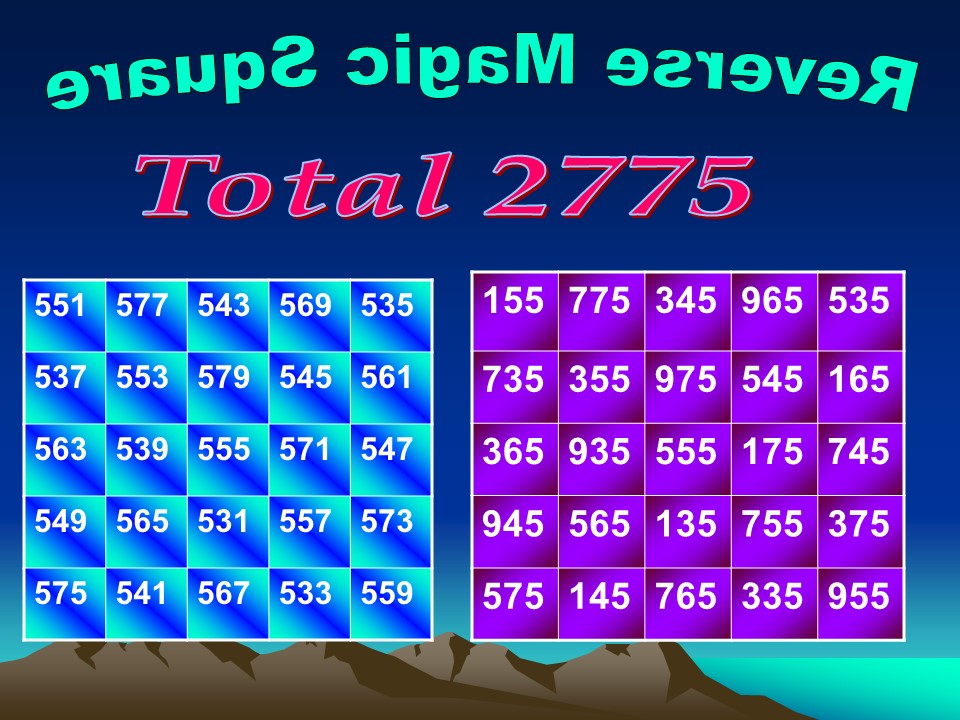
Reverse Magic Square is a very special kind of Magic square.
All numbers in the left side magic square are written in the reverse order in the right side magic square.
Surprisingly both or giving the same total of 2775
Puzzle in a 4 x 4 Magic square
It is an interesting mind boggling puzzle.
There is a Magic square given in the left picture. In the right side picture all numbers are replaced by letters.
Normally all Horizontal, vertical and both diagonal totals are equal to 34
ie. A+B+C+D = 34, E+F+G+H = 34 etc….and A+E+P+W = 34 ….
Along with that if you select a set of four alphabets like E+H+R+Y =34.
E+F+R+S = 34 ……..
You can select so many sets of four numbers such that their total comes to 34. Remember there are around 80 different methods.
Try your best to get them
Alphabet Magic square
In a very novel method, constructed this very special Magic square
Session at School
Teaching of “FUN MATHS AND MIND GAMES” IN AN INNOVATIVE METHOD
Programmes conducted
Date Venue Students Attended
11-09-06 Thiagarajar college, Madurai (Inauguration of Maths Club) 100
08-12-06 Rotary club, Madurai West 20
11-12-06 Madurai Menakshi Matriculation School, Madurai (11th,12th) 300
27-12-06 Sri Ramana Madam, Tiruchchuli (Birth place of Sri Ramanar) 25
04-01-07 Madurai Distict Level Science Exhibition 200
13-01-07 “Top Kids’ programme in Madurai Fortune Pandyan Hotel (Sponsored by Dr.Deep, Madurai) 50
02-03-07 Rotary club, Madurai North, Fortune Pandyan Hotel 25 13-03-07 Madurai Kamaraj University Teacher’s association 15
22-03-07 Thiagarajar college, Madurai (before NAAC committee 100 27-03-07 Sourashtra College for men (Maths club inaguraion) 175
16-05-07 T.V.S.Lakshmi Matriculation Higher Secondary School,
Madurai(Summer camp) 20
01-06-07 At Veeravanallur Indira Mat.Hr.Sec.School 20 22-07-07 Jain vidyalaya, Madurai 100
09-08-07 Yadava College, Madurai (Young scientist programme – by HRD/DST) 60
13-08-07 Rotary Metro, Madurai (Pasumalai Gateway Hotel) 50
14-09-07 Rotary West Madurai, Madurai (Sangam Hotel, Madurai) 25
28-09-07 Thiagarajar college of Engineering ( Tamilnadu-Kerala Mathematics Assn 3 days conference on Discreate Mathematics) 100
04-12-07 Rotary South, Madurai at Fortune Pandyan Hotel 15
20-12-07 Sivakasi Nadar women’s college, Poovandhi, near Madurai 250
27-12-07 Ramakrishna Madam, Tiruppalai, Madurai (For teachers only) 15
06-02-08 Science Exhibition,Birla Planitarium,Chennai (3 days) 300
22-03-08 King’s college of Engineering, Thanjavur (2 Sessions) 500
16-04-08 Vellammal Mat. Hr. Sec/ School, Viraganur, Madurai (Summer camp) 60
22-04-08 Leonard Hearing impaired school, Viraganur, Madurai 40
22-04-08 Vellammal mat.Hr.Sec.School, Tiruppuvanam, Madurai (for Teachers) 10
15-05-08 “JAYA TV” DIRECT TELECAST PROGRAMME
(Dial Jaya TV- One Hour)
22-05-08 Young Scientist programme (By dept of HRD/DST) (American college) 80
29-06-08 DD TV/ MADURAI- TELE SERIAL “KANNIKKILE PULI” (Shown in DD I Podigai Eight TIMES within two years)
04-07-08 Oxford Matriculation Hr Sec. School, Sivagangai 300
08-07-08 Fatima college, Madurai (Maths club inauguration) 400
30-07-08 Lady Doak College,Madurai( Maths club inauguration 500
03-08-08 Living Word Church, Madurai 80
29-08-08 Maths. Exhibition, Poovandhi Women’s college, 500
18-10-08 Zonal Railway Training centre, Tiruchy 30
20-10-08 Ayyappan Temple, Crafort, Tiruchy 50
05-11-08 Meenakshi Sundaraeswarar Girl’s Higher Sec. School, Madurai- 300
15-12-08 To 18-12-2008 SIX SCHOOLS in the Kalppakkam Atomic Centre Nagar, 2000
29-01-09 Zigma Mat. Hr. Sec. School, Madevakkam, Madras 160
30-01-09 Government Hr.Sec.School, Madevakkam, Madras 200
07-02-09 Tamilnadu Science and Tech. Park, Birla Planetarium, Tiruchi 100
21-02-09 St.Joseph deaf and dumb School, Manamaduri 50
16-04-09 Tamilnadu Science and Tech. Park, Birla Planetarium, Tiruchy 75
26-04-09 KUMBAKONAM RAMANJUJAN MEMORIAL MATHS RESEARCH CENTRE, SASTRA, ON RAMANUJAN’S MEMORIAL DAY 100
13-05-09 Vellammal Mat.Hr.Sec.School, Virganoor, Madurai (Summer Camp) 40
28-02-09 Vellammal Engg,college, (Science Exhibition) 200
19-03-09 Vinayaka Mat.Hr.Sec.School, Sivakasi
(Cover story for SIVAKSI TIMES MAY 2009) 150
03-04-09 IN THE SCIENCE EXHIBITION TRAIN – AT MADURAI
STUDENTS 200
(Science express team at the mathematics training session. Conducted by T.R.Jothilingam, Station Master, Madurai )
03-04-09 FOR THE VOLUNTEERS OF THE SCIENCE EXHIBITION
(In the science exp Train at Madurai Jn. 20
29-03-09 Lady Doak college YOUNG SCIENTIST PROGRAMME
2 DAYS (HRD/DST) 100
15-07-09 Lady Doak College, Maths club inauguration 300
18-08-09 T.E.L.C. Girls Higher Secondary School, USILAMPATTI 400
29-11-09 Madurai Readers’ club 50
06-12-09 Bharathiar Govt. Hr.Sec.School, Veeravanallur 300
11-3-10 Thiagarajar school of Management, Madurai 200
20,21-3-10 Zigma matriculation Higher secondary School, Chennai 100
11,12-7-10 Science Exhibition by DST/Delhi at Yadhava college, Madurai 500
28-7-10 Vellammal Engg. College “SCIENCE UTSAV 2010”, Madurai 200
12-8-10 The American College, Madurai, Maths club Inaguration 200
17-8-10 Government Saliar Higher Seconday School, Chattirappatti,
Rajapalayam. 400
19-8-10 Thiagarajar College of Engineering, Madurai
( Ramanujan Maths Colloquium ) 50
05-12-2010 Madurai VAIGAI CLUB ( RLY) 50
31-12-2010 Madurai Zageer”s party 40 31-12-2010 Madurai friends house 20
22-03-2011 Leonard Hearing impaired school, Virganoor, Madurai, 60 (Lips movement method)
- Kendiriya Vidyalaya, Indian Institute of science, Bangalore
Two sessions 400
- Kendirya Vidyalaya Sangathan, (KVS Head Quarters)
(For KVS principals and for KVS PG & UG Maths teachers) 15
26-4-2011 Ramanujan Museum and Math education centre Chennai 50
24-5-2011 Madurai singarathoppu meeting 30
3 – 6- 2011 Science Express , Madurai Junction (For volunteers) 30
21-6-2011 SBOA school, Nagamalai, Madurai 400
9/10-8- 2011 Kuppam – Agastya International Foundation (Teachers) 20
30 – 8 2011 Vivekananda Institute of Engineering for women, Tiruchengode 300
13-10-2011 Wards of Railway employees , Madurai 30
15-11-2011 Vikaasa School, Madurai 250
24-11-2011 Madurai, Muthupatti, Refersher course for Teachers
“Teaching arithmetic to Visually impaired” 30
2/3-02-2012 Madurai, Muthupatti special course for the teachers of the
Visually impaired schools of Tamil Nadu 35
7-2-2012 Students of eighth standard at Nilaiyur N.K.Kuppain school 70
14-2-2012 Chennai, National Institute of Visually Handicapped, Poonamallee 25
17-2-2012 Madurai, Sundarrajanpatti, Visually impaired school 30
9-3-2012 Rotarty club meeting, Hotel Sangam, Madurai 20
7-4-2012 Madurai Institute of Technology, Madurai 250
13-5-12 Natrankal – A Summer camp for students at Tirunagar 50
15-5-12 Sourashtra Chamber of Commerce – a spl family meet 50
21-5-12 Sourashtra Chamber of Commerce- Free classes proposed 50
22-5-12 Young Scientist programme – Thiagarajar College, Madurai 80
( Hosted by Dept.of Science and Technology, Newdelhi.)
9-7-12 Bharathiyar Higher Secondary School, Viravanallur 60
17-7-12 Vellammal Mat. Hr.sec.school, Madurai 100
19,20-7-12 Science Exhibition, Railway Mixed School, Madurai 200
7-8-12 Kamatchi Mat.Hr.Sec.School. Tuticorin 100
18-8-12 Science Express at Kudal Nagar Railway station 100
23-8-12 Railway Mixed Hr Sec. School, Madurai 120
31-8-12 Nilaiyur VAO programme 10
4-9-12 Dharangadhara Chemical Works school, Tiruchendur 200
8-11-12 Railway Mixed School, Madurai (9th an 10th Students) 100
9-11-12 Railway mixed School, Madurai (11th and 12th) 100
20-11-12 District Science Centre, Tirunelveli (Sponsored by TEST)
(Morning session 120 , Evening session 120) 240
- Railway Mixed School, Perumbur, Chennai“ 150
30-11-12 Railway Mixed School, Perumbur, Chennai 150
29-11-12 Chennai Egmore Museum 75
25-12-12 Dhanalakshmi Engg. College, Tambaram, Chennai. 200
5 -2-13 Mannar college, Madurai 50
8-2-13 Mount Litra Zee school , Shalavandan 20
12-2-13 K.L.N.Mermorial Polytechnic, Madura 100
12-2-13 K.L.n.Teacher Training College, Madurai 100
12-3-13 Mother Theresa Teacher Training college 100
6 – 4- 13 Mount litra Zee School Annual Day – Chief Guest 100
26-4-13 SASTRA – KUMBAKONAM, Ramanujan Memorial day 150
10-6-13 Usilampatti college 50
11-8-13 Virvanallur Bharathiar school 50
8-10-13 Elango Corporation School, Madurai 100
22-10-13 Madurai Gandhi Museum 20
28,29-12-13 Madurai Sourashtra High school Maths Exhibition 200
11,12-1-14 Madurai Gandhi Museum (Maths Exhibition with my own products) 500
15-1-14 Madurai Sourashtra High School, 40
16-1-14 Madurai Sivasakthi Illam 30
23-1-14 Erode Railway Mixed High School 300
9-2-14 Tiruppalai, Madurai 20
13-2-14 Kilakkari Islamiah School 200
26-2-14 Sourashtra women college 200
28-2-14 KLN college of Engg 120
4-3-14 Sourashtra times tv Serial 25
26-4-14 Sourashtra times TV serial -2 35
18-7-14 Inaguration of Commerce club: Thiagarajar college 160
25-7-14 Thiagarajar college of prospetors 120
27-7-14 Chellur Raghunath 50
8-8-14 CEOA school, Kanagavel colony 160
16-8-14 CEOA School, Madurai Main building, 120
25-8-14 N.K.Kuppaiyan Rathnamani memorial school, Nilaiyur, Madurai 100
27-8-14 Chellur Raghunath 40
5-9-14 SPVM school, Madurai 80
11-9-14 Erode Railway school 200
12-10-14 Coimbatore Gujarati samaj 50
28-10-14 SACS MAVMM engg college 200
23-5-15 Sou.Chamber of commerce 30
1-7-2015 Vivekananda Engineering college for women, Thiruchengodu 500
2-7-2015 —————- do —————————————————- 500
3-7-2015 ————– do ——————————————— 500
13-7-2015 Vivekananda college for women, Arts and science college 200
22-12-2015 Ramanujan Museum, Chennai 80
19-2-2016 Nilaiyur School. Madurai (2 sessions) 100
23-2-2016 Kavibharathi School, Chennai (2 sessions) 160
06-05-2016 Madurai Singaraththoppu 50
25-5-2016 Kanniyakumari Vivekananda Kendra Teachers training Program 100
26-5-2016 ———do————- 100
27-5-2016 Kanniyakumari Vivekananda Kendra Teachers training Program 100
28-5-2016 —–do——
29-5-2016 —–do—–
MATHS EXHIBITION CONDUCTED AT VIVEKANANDA
KENDRA , KANNIYAKUMARY ON 29-05-2016
29-6-16 Vivekananda College of Engg., Tiruchengode 500
30-6-2016 –do—- 500
5-1-2017 sengalvarayan Polytechnic, Kanchipuram 100
6-1-2017 Sengalvaraan Poly technic,Chennai verperi 200
6-1-2017 Sengalvarayan High school, Chennai verpery 200
12-1-2017 N.K.Kuppian Rathnamani Meorial school, Madura nilayur 200
7-2-2017 Sattur S.R.memorial arts college, sattur 500
20-2-2017 Vadakkam patti Govt. High school, Chekkannoorani 100
10-4-2017 Priest house in Bangalore 30
24-04-2017 Vivekananda Kendra summer Camp, Tirupparankundram 50
06-05-2017 Vandiyur tution center 30
26-5-2017 Vivekananda Kendra teachers orientation program 110
27-5-2017 —–do —- 110
30-5-2017 Teachers orientation program Nilaiyur Nkk School, Madurai 40
6-7-2017 Government Girls Higher Secondary school, Rajapalayam 150
6-7-2017 Government Girls Higher Secondary school, Chattirappatti 50
26-7-2017 Pramathi Hillview Acadamy CBSE school, Mysuru 200
8-8-2017 Saint Claret High secondary school, Karumathur 300
7-9-2017 Burnpur school, Madhya predesh (For teachers orientation) 50
9-9-2017 Indore school, Madhya predesh (Teachers orientation Program) 50
9-9-2017 Indore Emerald Heights International school , M.P. 50
26-4-2018 Kumbakonam Sourashtra sabha 50
8,9,10-5-2018 Vivekananda Kendra, Madurai 50
4-7-2018 Nayagi vedapadasala, Madurai 40
17-5-2018 Sourashtra sabha, Hosur 40
1 – 8 2018 — Attended Teachers’ Orientation Camp at Dibrugarh 120 2 – 8 2018 — do — 80
3 – 8 -2018 – do — 40
4-8-2018 Vivekanada Kendra Vidyalaya, Satia 120
4-8-2018 Vivekanada Kendra Vidyalaya, Roing Arunachala Predesh (evening ) 120
5-8-2018 Vivekanada Kendra Vidyalaya, Roing Arunachala Predesh (Morning) 120
6-8-2018 Vivekanada Kendra Vidyalaya, Bokulani (NEEPCO power plant) 150
7-8-2018 Vivekanada Kendra Vidyalaya, Tingrai 150
8-8-2018 Vivekanada Kendra Vidyalaya, Tinsukia 100
28-8-18 Vivekanada Kendra Vidyalaya, Guwahathi 100
29-8-18 Vivekanada Kendra Vidyalaya, Suklai 120
30-8-18 Vivekanada Kendra Vidyalaya, Kajalgaon 100
31-8-18 Vivekanada Kendra Vidyalaya, Nalbari 200
1-9-18 Vivekanada Kendra Vidyalaya, Demaji 200
3-9-18 Vivekanada Kendra Vidyalaya,Dibrugarh 100
4-9-18 Vivekanada Kendra Vidyalaya, Sivasagar 100
5-9-18 Vivekanada Kendra Vidyalaya, Majuli 100
6-9-18 Vivekanada Kendra Vidyalaya, Golaghat 100
7-9-18 Vivekanada Kendra Vidyalaya, Tezpur
Palindromic Magic Square (விகடகவி மாயச் சதுரம்)
A palindrome is “a word, phrase, or sequence that reads the same backwards as forwards“, example madam
We have come up with a new idea of forming palindrome magic square with special feature of repeated numbers along the diagonals!
This is a sample 5 x 5 Palindrome Magic Square. We have also done the same for higher orders including 7 x 7, 11 x 11, and so on! Happy exploring!!
Note: விகடகவி மாயச் சதுரம் in Tamil means Palindrome Magic Square
Diabolic Magic Square
The above 4 x 4 Magic square gives a total of 34 across all rows (horizontal), columns (vertical) and both diagonals. ( 4 + 4 + 2 = 10 methods)
Along with that, each distinctly colored 2 x 2 square will give a combined total of 34 each.
Additionally, the four corners, 4 middle numbers will give a total of 34.
We can select, 4 particular numbers and come with a total of 34 in more than 60 different ways.
Explore it for yourself and enjoy!!
Done a World’s biggest 1999 x 1999 Diamond inlaid magic square ( All numbers from 1 to 39,96,001 used) Example: 21 x 21 Diamond inlaid magic squares is given here. (With numbers 1 – 441 )
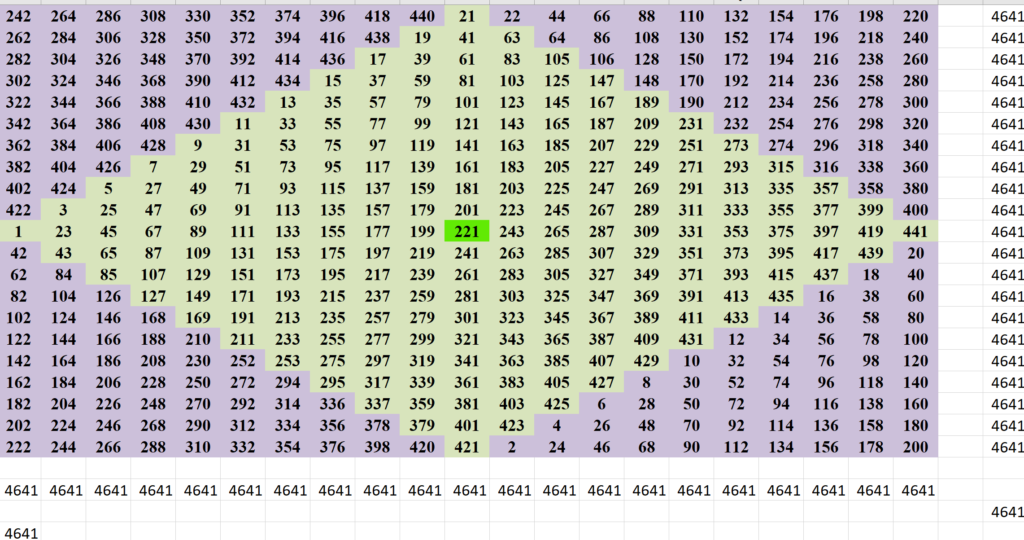
Diamond inlaid magic square is a very special magic square. It will have all odd numbers placed in the center in a Diamond shape and all even numbers distributed in four seperate triangular shape in the four corners.
In the above 21 x 21 diamond inlaid magic square, all the numbers from 1 to 441 are used. All the vertical, Horizontal and both diagonal totals are equal to 4641.
Surprisingly around the center number 221, all the diagonally opposite postioned numbers, and symetrically opposite positioned numbers will give a total of 442. There are 441 – 1 = 440 / 2 = 220. We can get it in 220 different methods.
I have done a 1999 x 1999 Diamond inlaid magic square in which all the numbers from 1 to 39,96,001 are used. All Horizontal, vertical and both diagonal totals will be 399,40,03,999. ( Three hundred ninty nine crores, forty lakhs, three thousand and nine hundred and ninety nine) or 3,994,003,999 ( Three Billion, 994 million, three thousand nine hundred and niniety nine)
Thanks to the Almighty for giving me the idea, guided me, till the final execution to make it a reality.