
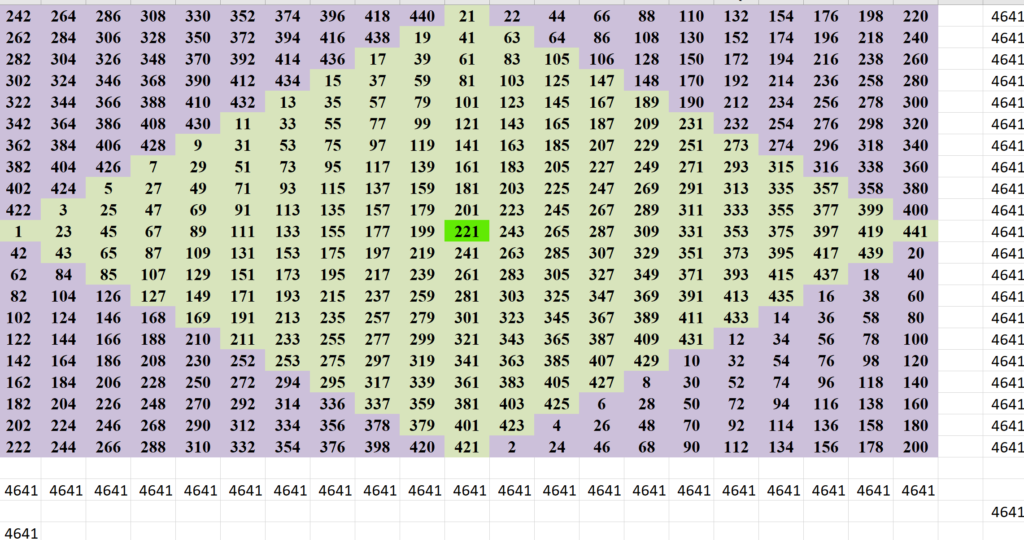
I have done Magic squares inside a magic square from 5 x 5, 6 x 6 ……upto 199x 199 and 200 x 200


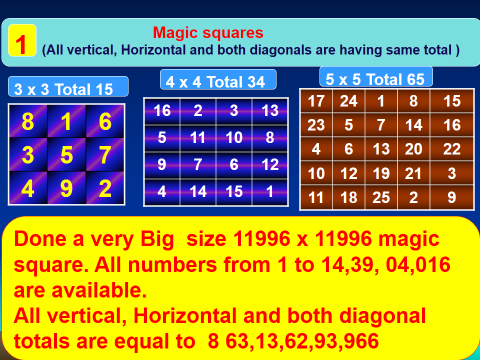
One very interesting fact about the above magic square. It contains all numbers from 1 to 14,39,04,016. Many of the numbers are having nine digits.
If we write a number in a 3 cm width square space, the total length of writing the entire numbers will be 431712048 cms. It means 4317120 meteres or 4317 kilo meteres.
India’s longest train that runs from Kanyakumari to Dibugarh is covering the entire distance of 4273 km in 74 hours.
If we start writing the numbers from Kanyakumari it will go beyond Dibrugarh and beyond by 44 kilometers. It is really a very interesting fact.
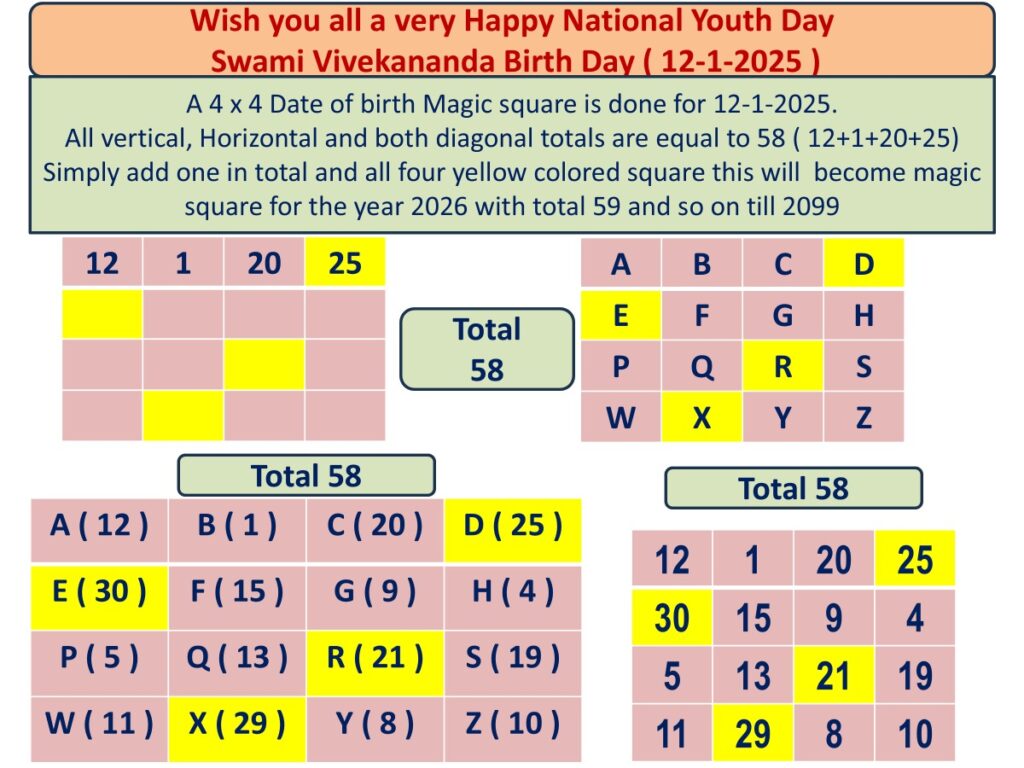
4) Count all numbers 12 + 1 + 12 + 25 = 58
5) In a separate 4 x 4 square replace all numbers as A, B, C, D etc as shown in the right side square Now A = 12, B = 1, C = 20 and D =25. Rest all value we have to find out.
6) Now count all the numbers of 58 in the top and make it a single digit. i.e. 5 + 8 = 13, once again 1 + 3 = 4 and place it the H square. ( H value is 4.)
7) Now add B + C i.e. (1 + 20 ) = 21 and split it into two parts. Let it be 11 and 10. Now Place them in W and Z i.e. W=11 and Z=10.
8) Now remember, in a magic square all the vertical, Horizontal and both Diagonal totals are equal and for this square it will be 58.
9) To find S, add D + H + Z and subtract it from 58. i.e.58 – (25 + 4 + 10) = 58 – 39 = 19. Hence S = 19
10) Now to find the value of Q and G, add ( D + W ) and deduct it from 58. ie. 58 – (11 + 25 ) = 58 – 36 = 22 . Make it two parts. Let it be 13 and 9. Hence place Q = 13 and G =9.
11) Now to find F and R, add A and Z and deduct it from 58. i.e.58 – (12 + 10) = 58 – 22 = 36 . Spilt it into two parts. Let it be 15 and 21. Place F =15 and R= 21
12) Now to find E, add ( F + G + H ) and deduct it from 58. i.e. 58 – ( 15 + 9 + 4 ) = 58 – 28 = 30. Hence E = 30.
13) Now to find P, Add ( Q + R + S ) and deduct it from 58. i.e. 58 – (13 + 21 + 19) = 58 – 53 = 5 . Hence P = 5.
14) Now we found the values of A, E, P, W. Let us check whether A + E + P + W = 58. 12 + 30 + 5 + 11 = 58. OK.
We can proceed further.
15) To find X, add B + F + Q and deduct from 58. I.e. 58 – ( 1 + 15 + 13 ) = 58 – 29 = 29. Hence X = 29.
16) And finally to find Y, add C + G + R and deduct it from 58. i.e. 58 – ( 20 + 9 + 21 ) = 58 – 50 = 8. Hence Y= 8.
17) Now Finally add W + X + Y + Z = 11 + 29 + 8 + 10 = 58.
Waaaaw!!! You have got the magic square for 12 – 1 -2025, with all vertical, Horizontal and Both diagonal totals are 58.
Remember.. You can make millions of magic squares for this date with the same total 58




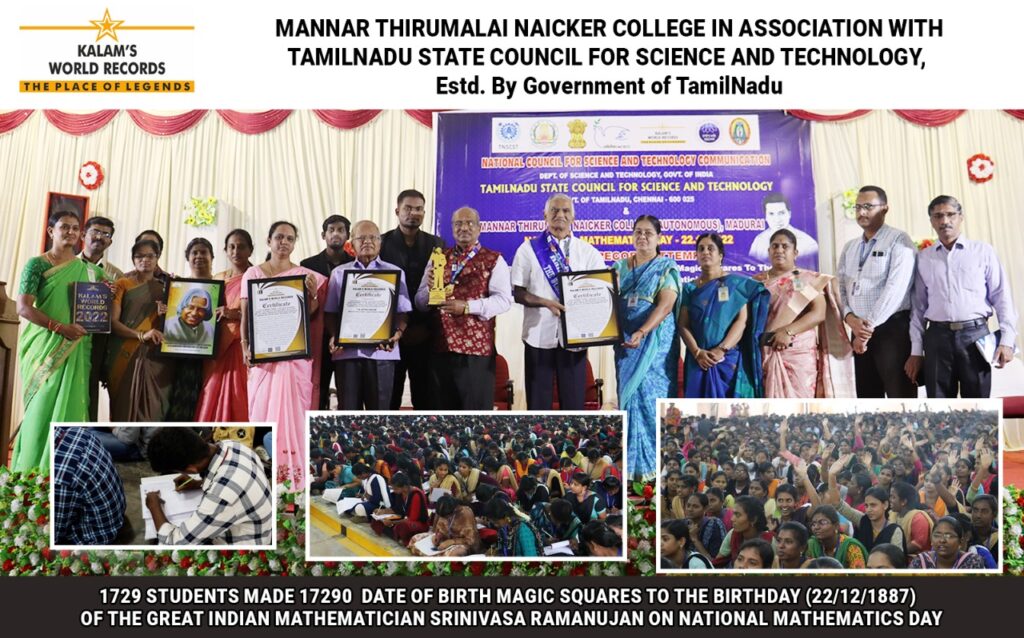
I conducted a mega World Record event at Madurai with the participation of 1,729 students of the Mannar Thirumalai Nayakar college in Madurai making 17,290 individual date-of-birth Magic Squares to the date of birth of the Great Indian Mathematician Srinivasa Ramanujan (22nd December 1887).
This mega World Record event the was certified by Kalam’s World Records based in Chennai.
This is the most fitting tribute to the Great Indian mathematician Srinivasa Ramanujan on his 135th birth anniversary celebrated worldwide.

Here is a video which covers the event (audio is in native language Tamil though).
The following number puzzle is dedicated to the Great Indian Mathematician on his 135th year of Birth Anniversary celbrated all over the world.

Honoring the Great Indian Mathematician Srinivasa Ramanujan on his 102nd Remembrance day — An Unique Puzzle by www.jollymaths.com
This is a Unique Puzzle that makes magic squares for his date of Birth on 22-12-1887 and for his 102nd Remembarance day, today(26-4-2022)
On Left side we are having a brown color magic square for 22-12-1887 giving a total of 139 in all vertical, Horizontal and both diagonals.
On the right side we are having a light green color magic square for 26-4-2022 giving a total of 174 in all vertical, Horizontal and both diagonals.
And the balance squares are filled with compensatory numbers.
The final form is a 9 x 9 Magic square is giving a total of 313 in all vertical, Horizontal and both diagonals.
