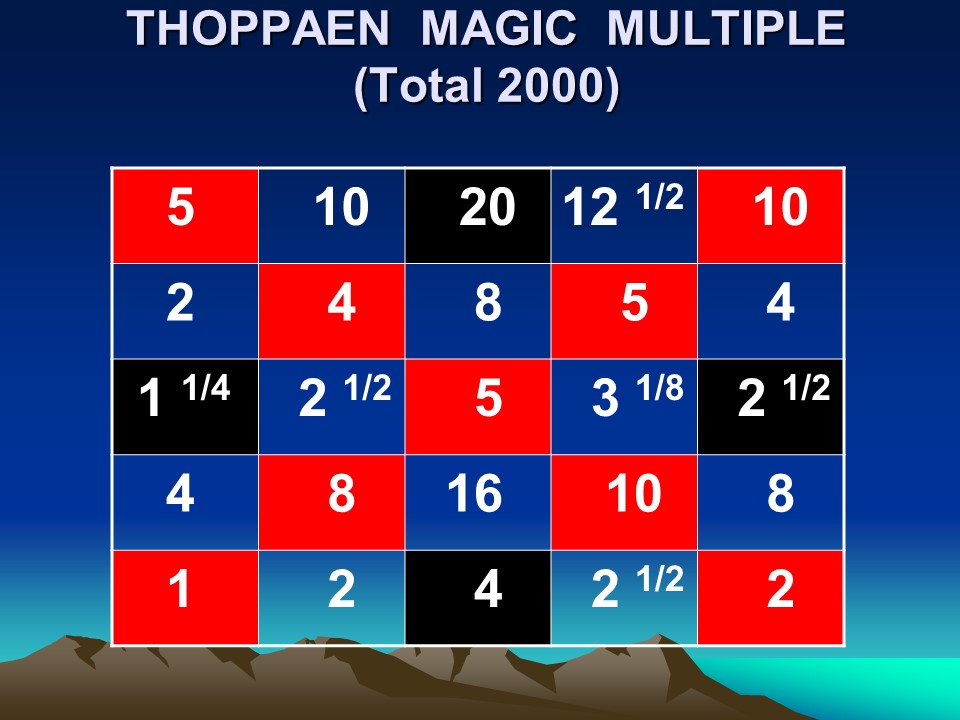
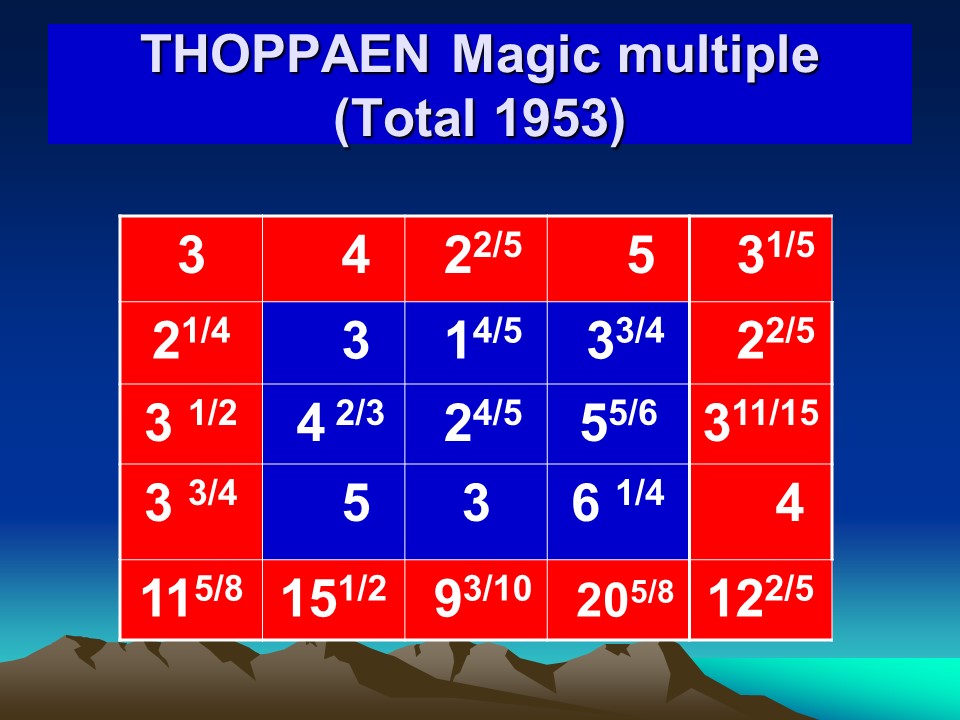
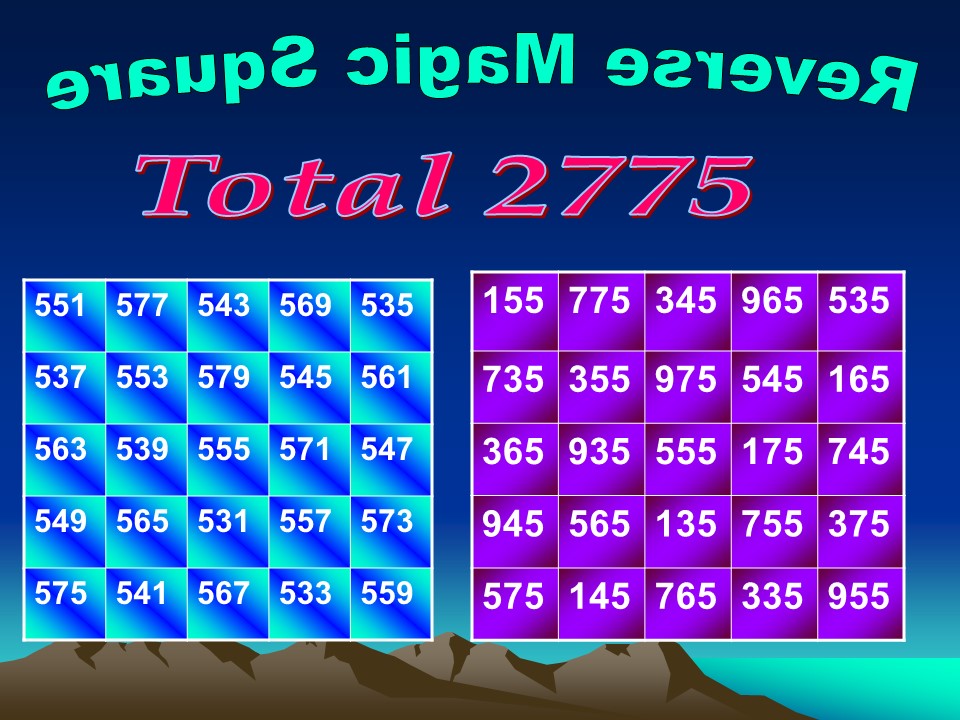
I conducted a mega World Record event at Madurai with the participation of 1,729 students of the Mannar Thirumalai Nayakar college in Madurai making 17,290 individual date-of-birth Magic Squares to the date of birth of the Great Indian Mathematician Srinivasa Ramanujan (22nd December 1887).
This mega World Record event the was certified by Kalam’s World Records based in Chennai.
This is the most fitting tribute to the Great Indian mathematician Srinivasa Ramanujan on his 135th birth anniversary celebrated worldwide.

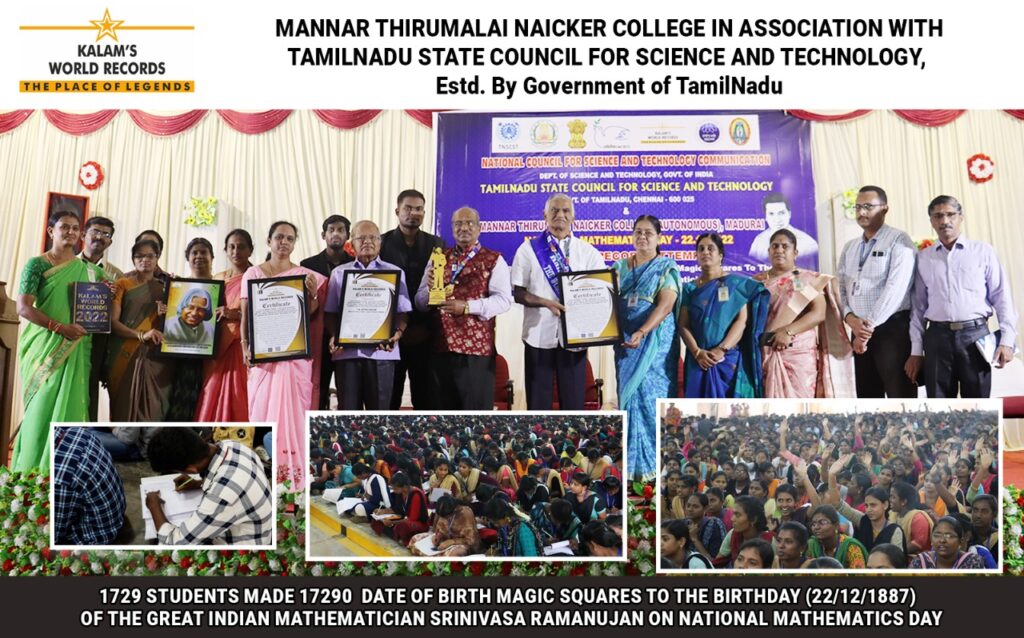
Here is a video which covers the event (audio is in native language Tamil though).