Introduction – Properties of Magic Square
Magic squares are made in 3 x 3 squares, 4 x 4 squares, 5 x 5 squares, etc, filled with numbers. After filling all the numbers, all the VERTICAL, HORIZONTAL AND BOTH THE DIAGONALS’ TOTALS ARE EQUAL. And this total will be {(1+n2)/2}*n. (Where n = number of rows or number of columns)
In simple format, the total will be the lowest number added togetheer withthe highest number, then divided by two, and them multiplied by the number of rows. This is the minimum condition for any magic square.
Generally a 3 x 3 Magic square is filled with numbers 1 to 9 ( 9 = 3 x 3), a 4 x 4 magic square with 1 to 16 ( 16 = 4 x 4 ) and a 5 x 5 magic square with 1 to 25 etc. In general a ‘n’ x ‘n’ magic square is filled with 1 to n2 numbers.
It will have ‘n’ rows and ‘n’ columns and totally there are n2 small squares.
Generally 1 to n2 numbers are used to form the magic squares. In special cases we can use fractions, zero, negative numbers and squares, cubes also
We can make 3 x 3, 4 x 4, 5 x 5 etc. magic squares for a particular given number like your birth year and for a given numbers also.
I hope you will find these information useful. Note that these contents are copyrighted and cannot be copied without the written permission from the author. email me
How to make a 3 X 3 Magic Square ?
1. Draw an empty 3 x 3 square. It is the boundary for 3 x 3 magic square
2. We are going fill all numbers from 1 to 9, in the nine squares.
Always write number ‘1’ in the upper middle square
3.Always write the next number one square right and one square above, AND WHEN IT GOES
A) Beyond boundary in the upper side, write it vertically downmost square
B) beyond the boundary in the right side, write it in the horizontally leftmost square
C) When the square is already filled with a number , just step down one square vertically and write the number
4. and after the top row rightmost square always write the next number one square vertically below
5. With these simple techniques you can make any ODD NUMBER MAGIC SQUARE like 5 x 5, 7 x 7, 9 x 9 etc. etc.. upto any highest odd number in the world.
3 x 3 Magic square: Total 15
3 x 3 Magic square Total 2025
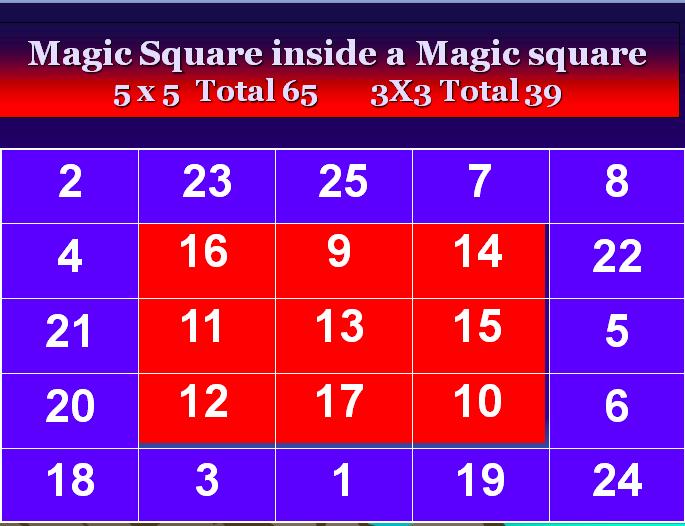
5 x 5 Magic square Total = 65
( 1+25 = 26/2 = 13 x 5 = 65 )
5 x 5 Magic square with magic sum 2025
[table “5_by_5_total_2025” not found /]
5 x 5 Magic square inside a Magic Square
How to make a 4 X 4 Magic Square ?
1. Draw a 4 x 4 empty square.
2. Draw the two diagonals.
3. Count all squares from the top left towards the right. (Total 16)
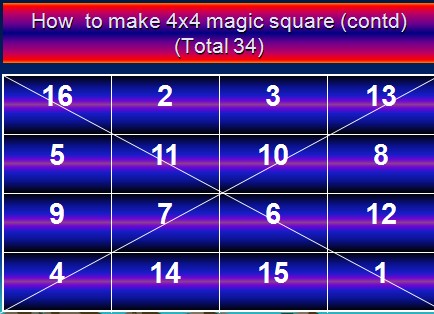
4. Now start writing numbers 1 to 16 from the top left square . Count all squares , and write numbers only in the blank squares. Do not write numbers in the squares with diagonal lines. (2, 3, 5, 8, 9, 12, 14, 15 are to be filled, as shown in the image below).
5. Now start writing the numbers from the bottom most right square towards left, count all squares BUT WRITE NUMBERS ONLY IN THE SQUARES HAVING DIAGONAL LINES ONLY. (1, 4, 6, 7, 10, 11, 13, 16 are to be written (as shown in the image below).
6. Magic square 4 x 4 ready . All vertical, Horizontal and both diagonals are equal to 34.
7. This method will be applicable for 4 x 4 only.
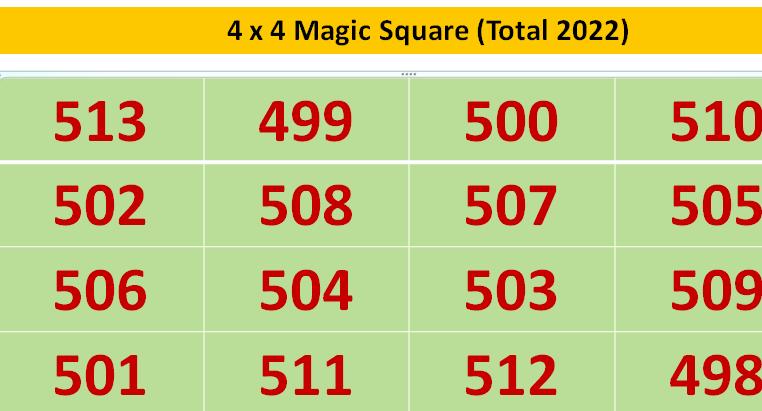
By suitably changing the starting number (which was 1 in this example), we can make Magic squares of any total. For example, if we start with 498, we can get a 4 x 4 magic square with Total 2022 as follows:
Any Order – Odd
This procedure is same as that of making a 3 X 3 magic square, except that we start with a n X n square initially and start filling numbers following the same rules that we followed for making a 3 X 3 Magic Square.
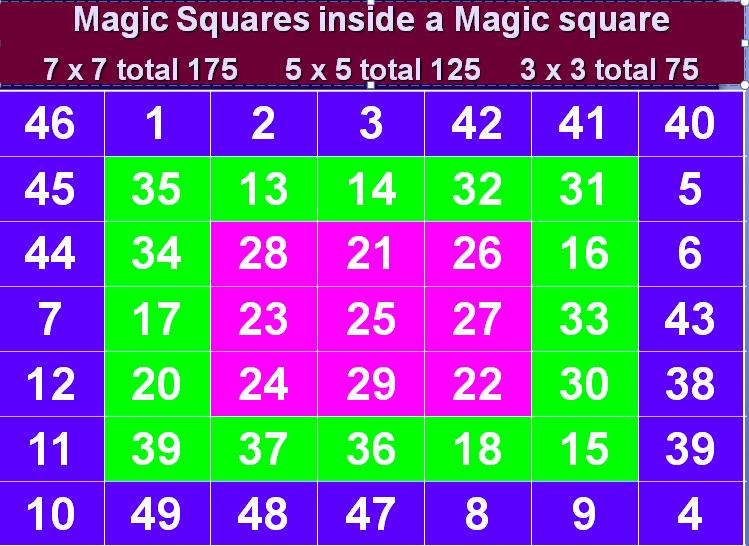
7 x 7 Magic square inside a Magic Square
Any Order – Even
As such there is no known, GENERAL methodology to obtain an even order magic square upto any order.
Word Magic Square
As such there is no known, GENERAL methodology to obtain an even order magic square upto any order. Anyhow you can make these magic squares with trial and error methods.
An example is given to you to get an idea.
Total 45
| 25 | 2 | 18 |
| 8 | 15 | 22 |
| 12 | 28 | 5 |
In the above 3 x 3 magic square, all totals are 45. Take the upper middle square, 2 (TWO) written in alphabhats will have three letters and in the corresponding square shown down you have to write the number three. Likewise all numbers are to be written and according to the alphabhats available. AMAZINGLY THIS WILL ALSO BE A MAGIC SQUARE of total 21.
Total 21
| 10 | 3 | 8 |
| 5 | 7 | 9 |
| 6 | 11 | 4 |
OTHER SUCH INTERESTING– Special Magic Squares
As such there is no known, GENERAL methodology to obtain any other Magic Sqaure
- Diamond magic square
- Swastika magic square
- Spell magic square
- Date of birth magic square
- Biography magic square
- Reverse magic square
- Upside down magic square
- Mirror magic square
- 1800 turned Magic square
- Palindrome Magic square
- Magic squares inside a magic square
- Upside down and Mirror Magic square
- Diabolic magic square
- Multiplication Magic Squares
- Magic squares for a given year
- Completing a magic square when only any two numbers are given in any 3 x 3 or 4 x 4 or any other order
- 2 x 2 continuous magic squares
- 64 moves of a king in a chess board and the final path is a 8 x 8 magic square
- 64 moves of a knight in a chess board and the final path is a 8 x 8 magic square
- 64 moves of a rook in a chess board and the final paths is a 8 x 8 magic square